 Ya que Elenin ha producido tanto revuelo, que pienso es totalmente injustificado, nos servirá para hacer una práctica con el fenomenal programa Stellarium.
Ya que Elenin ha producido tanto revuelo, que pienso es totalmente injustificado, nos servirá para hacer una práctica con el fenomenal programa Stellarium.Stellarium es un programa gratuito de código abierto. Es capaz de mostrar un cielo realista en 3D, tal como se aprecia a simple vista, con binoculares o telescopio.
Sólo especifica las coordenadas y listo.
La practica va a consistir en añadir un cometa nuevo a su base de datos para poder seguirlo en el futuro con el planetario.
Para los que no lo conozcáis, lo podéis bajar de su página oficial: http://www.stellarium.org/es/
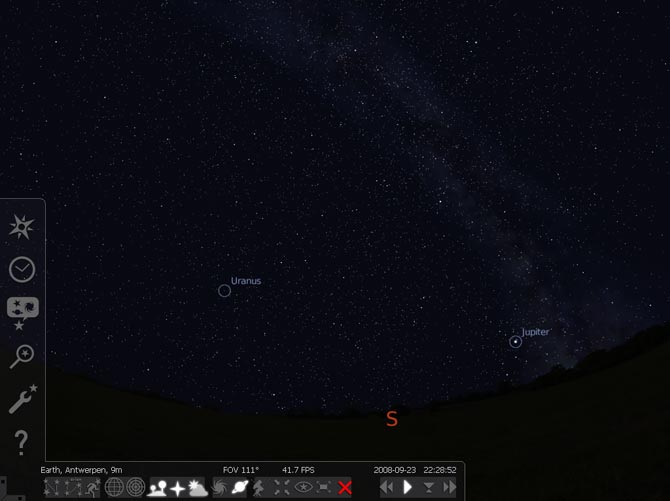
En el programa Stellarium, se pueden incluir los objetos de reciente descubrimiento, simplemente escribiendo sus elementos orbitales en el fichero de inicio del programa (.INI).
En primer lugar, localiza el archivo Stellarium/Data/ssystem.ini en Archivos de Programa. En este archivo se almacenan los elementos orbitales del Sol, La Luna, Mercurio, Venus, etc... en general de todos los cuerpos que vemos seguir una órbita desde la Tierra (satélites de otros planetas y asteroides, cometas...incluidos).
Edita el fichero con un editor de texto (Wordpad, p.ej) y vete al final del mismo. Incluye las siguientes líneas:
name = 2010X1/Elenin
parent = Sun
coord_func = comet_orbit
radius = 10
oblateness = 0.0
albedo = 1
lighting = true
halo = true
color = 1.0,1.0,1.0
tex_map = nomap.png
tex_halo = star16x16.png
orbit_Epoch = 2455635.5
orbit_SemiMajorAxis = -8379.16344923547
orbit_Eccentricity = 1.000057574878451
orbit_Inclination = 1.839430469894279
orbit_AscendingNode = 323.2333639750312
orbit_ArgOfPericenter = 343.7998575586238
orbit_MeanAnomaly = 359.9997690603867
absolute_magnitude = 10.0
slope_parameter = 4
orbit_TimeAtPericenter = 2455815.219562854138
orbit_visualization_period = 365.25
Graba el archivo de nuevo en el directorio. Inicia Stellarium y ya funcionará. Busca el cometa 2010X1/Elenin y localiza su trayectoria a lo largo de los días. Recuerda eliminar la atmósfera y variar otros parametros si es necesario por la hora o situación para hacerlo visible. El único problema es que no se conocen algunos elementos orbitales y la magnitud absoluta del cometa aparece como de 40 (en el programa Stellarium), cuando en realidad es de 10.
No hace falta decir que esto mismo es lo que hay que hacer para incluir cualquier objeto que deseemos. Podemos buscar los datos en diversos lugares especializados en Astronomía.
¿QUÉ SON LOS ELEMENTOS ORBITALES?
Las órbitas se definen según las leyes de Kepler. En base a estas leyes, los cuerpos en órbita recorren una trayectoria en forma de elipse, con el Sol en uno de los focos (1ª ley de Kepler), la linea que une el planeta o cuerpo con el Sol, en tiempos iguales, recorre areas iguales (2ª ley de Kepler) y el cuadrado del periodo de un planeta es proporcional al cubo de su distancia media al Sol (3ª ley de Kepler).
Kepler definió el "como", pero Newton definió el "cuanto".
A Newton se debe el descubrimiento de las leyes del movimiento y de las fuerzas que actuan sobre los cuerpos, y enunció la Ley de la Gravitación Universal definiendo que la Fuerza entre estos es "directamente proporcional a las masas e inversamente proporcional al cuadrado de las distancias". Es decir:
en la que Fg es la Fuerza de atracción entre dos cuerpos, M y m son las masas de esos dos cuerpos, r es la distancia entre ellos y G es la Constante de Gravitación Universal, cuyo valor es
LOS ELEMENTOS ORBITALES
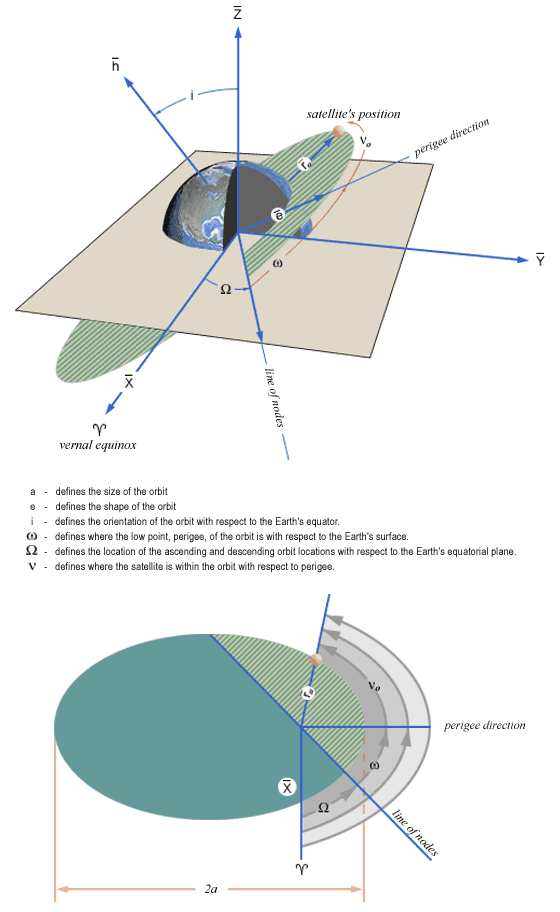
Son cinco magnitudes. Con ellas se define totalmente la forma, el tamaño y la orientación de la órbita de cualquier cuerpo. Además hay un sexto elemento para situar la posición del satélite en su órbita en un momento determinado. Los llamados "clásicos elementos orbitales" son:
El semi-eje mayor: es una constante que define el tamaño de la órbita (de la elipse). Se conoce comoa.
La excentricidad: es la constante que define la forma de la elipse. Se conoce como e.
La inclinación: es el ángulo entre el vector unitario K y el vector momento angular, h. Se conoce como i.
La longitud del Nodo Ascendente, es el ángulo, en el plano fundamental, entre el vector unitario I y el punto donde el satélite cruza el plano fundamental hacia el Norte (nodo ascendente) medido en sentido antihorario cuando se ve desde la cara Norte del plano fundamental. Se conoce como Ω.
Argumento del periapside. Es el ángulo, en el plano de la órbita del satélite, entre el Ω (nodo ascendente) y el punto del periápside, medido en el sentido de movimiento del satélite. Se conoce como ω.
Tiempo de paso por el periápside: el momento en que el satélite pasó por el periápside. Se conoce como T.
Estas definiciones valen para referirse a satélites orbitando la Tierra (con el sistema de coordenadas ecuatorial geocéntrico) o para definir órbitas de planetas orbitando el Sol, con sistema de coordenadas heliocéntricas. Tan solo se diferenciarán ambos tipos de satélites en la definición de de los vectores unitarios y en la definición del plano fundamental.
Cuando nos referimos a satélites terrestres, usamos la expresión perigeo en lugar de periápside. Ver aquí.
De la misma forma, cuando nos referimos a planetas orbitando alrededor del Sol, hablamos de perihelio en lugar de periápside.
Los elementos listados arriba no son los únicos, ya que se pueden usar otros, como la longitud del periápside, que es el ángulo desde I hasta el periápside medido al Este del Nodo ascendente (si existe), siendo conocido como Π y su valor es Ω + ω.
Si no hay periápside (como en el caso de las órbitas circulares) , no se definen ni ω ni Π .
Las órbitas se definen según las leyes de Kepler. En base a estas leyes, los cuerpos en órbita recorren una trayectoria en forma de elipse, con el Sol en uno de los focos (1ª ley de Kepler), la linea que une el planeta o cuerpo con el Sol, en tiempos iguales, recorre areas iguales (2ª ley de Kepler) y el cuadrado del periodo de un planeta es proporcional al cubo de su distancia media al Sol (3ª ley de Kepler).
Kepler definió el "como", pero Newton definió el "cuanto".
A Newton se debe el descubrimiento de las leyes del movimiento y de las fuerzas que actuan sobre los cuerpos, y enunció la Ley de la Gravitación Universal definiendo que la Fuerza entre estos es "directamente proporcional a las masas e inversamente proporcional al cuadrado de las distancias". Es decir:
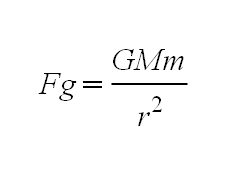 |
 |
LOS ELEMENTOS ORBITALES
Son cinco magnitudes. Con ellas se define totalmente la forma, el tamaño y la orientación de la órbita de cualquier cuerpo. Además hay un sexto elemento para situar la posición del satélite en su órbita en un momento determinado. Los llamados "clásicos elementos orbitales" son:
El semi-eje mayor: es una constante que define el tamaño de la órbita (de la elipse). Se conoce comoa.
La excentricidad: es la constante que define la forma de la elipse. Se conoce como e.
La inclinación: es el ángulo entre el vector unitario K y el vector momento angular, h. Se conoce como i.
La longitud del Nodo Ascendente, es el ángulo, en el plano fundamental, entre el vector unitario I y el punto donde el satélite cruza el plano fundamental hacia el Norte (nodo ascendente) medido en sentido antihorario cuando se ve desde la cara Norte del plano fundamental. Se conoce como Ω.
Argumento del periapside. Es el ángulo, en el plano de la órbita del satélite, entre el Ω (nodo ascendente) y el punto del periápside, medido en el sentido de movimiento del satélite. Se conoce como ω.
Tiempo de paso por el periápside: el momento en que el satélite pasó por el periápside. Se conoce como T.
Estas definiciones valen para referirse a satélites orbitando la Tierra (con el sistema de coordenadas ecuatorial geocéntrico) o para definir órbitas de planetas orbitando el Sol, con sistema de coordenadas heliocéntricas. Tan solo se diferenciarán ambos tipos de satélites en la definición de de los vectores unitarios y en la definición del plano fundamental.
Cuando nos referimos a satélites terrestres, usamos la expresión perigeo en lugar de periápside. Ver aquí.
De la misma forma, cuando nos referimos a planetas orbitando alrededor del Sol, hablamos de perihelio en lugar de periápside.
Los elementos listados arriba no son los únicos, ya que se pueden usar otros, como la longitud del periápside, que es el ángulo desde I hasta el periápside medido al Este del Nodo ascendente (si existe), siendo conocido como Π y su valor es Ω + ω.
Si no hay periápside (como en el caso de las órbitas circulares) , no se definen ni ω ni Π .

No hay comentarios:
Publicar un comentario